本页介绍了构建导航网格的第三阶段，即生成表示源几何体的可穿越表面（traversable surface area）的简单多边形（凸多边形和凹多边形）。轮廓仍然以体素空间为单位表示，但这是从体素空间回到向量空间的第一步。

源数据类：OpenHeightfield
构建器类：ContourSetBuilder
数据类：ContourSet 和 Contour

如果您需要了解此阶段执行的操作，请回顾处理过程概览。

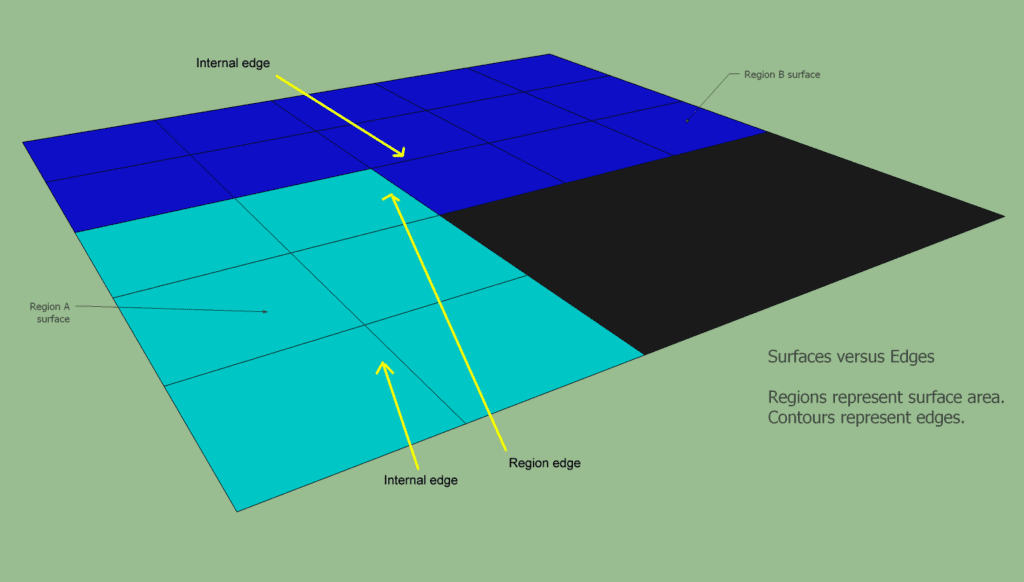
搜索区域边缘（Region Edges）

从开放高度场结构转向轮廓结构时，最大的概念变化是从关注span的表面（surface）转变为关注span的边（edges）。

对于轮廓，我们关心span的边。 有两种类型的边：区域边和内部边（region and internal）。 区域边是其邻居位于另一个区域中的span的边。 内部边是其邻居在同一区域中的span的边。

为了便于可视化，接下来的几个示例仅处理 2D，稍后我们将回到 3D。

在此步骤中，我们希望将边分类为区域边或内部边。这些信息很容易找到。我们遍历所有span，对于每个span，我们检查所有轴邻居，如果轴邻居与当前span不在同一区域中，则该边将被标记为区域边。

查找区域轮廓（Region Contours）

一旦我们有了关于哪些span的边是区域边的信息，我们就可以通过“遍历这些边”来构建一个轮廓。我们再一次遍历这些span，如果一个span有一个区域边，我们做以下工作:

首先面向已知的区域边，把它加到轮廓中。

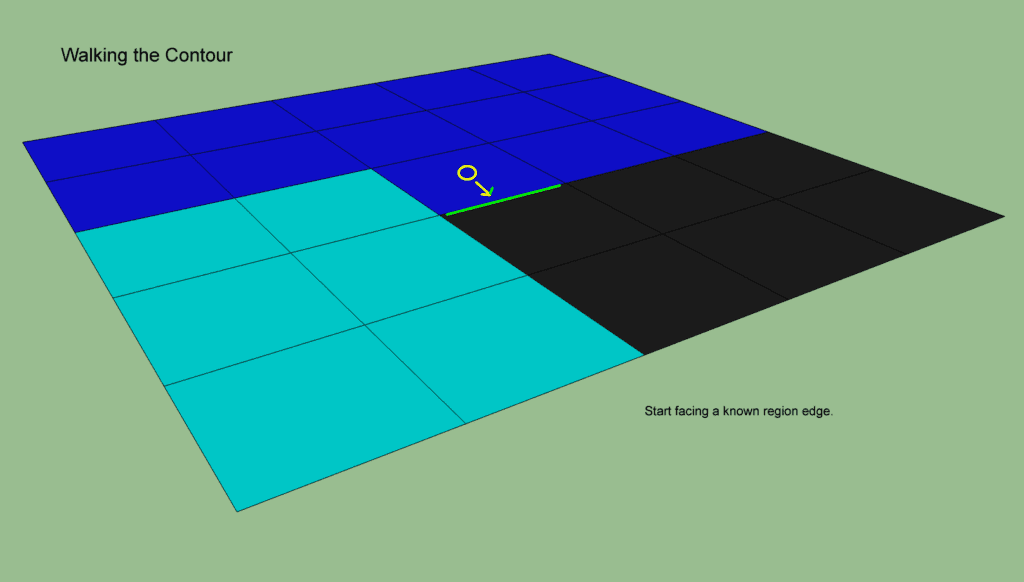
旋转90度，增加区域边到轮廓中，直到找到一个内部边。向前步进到邻居span。

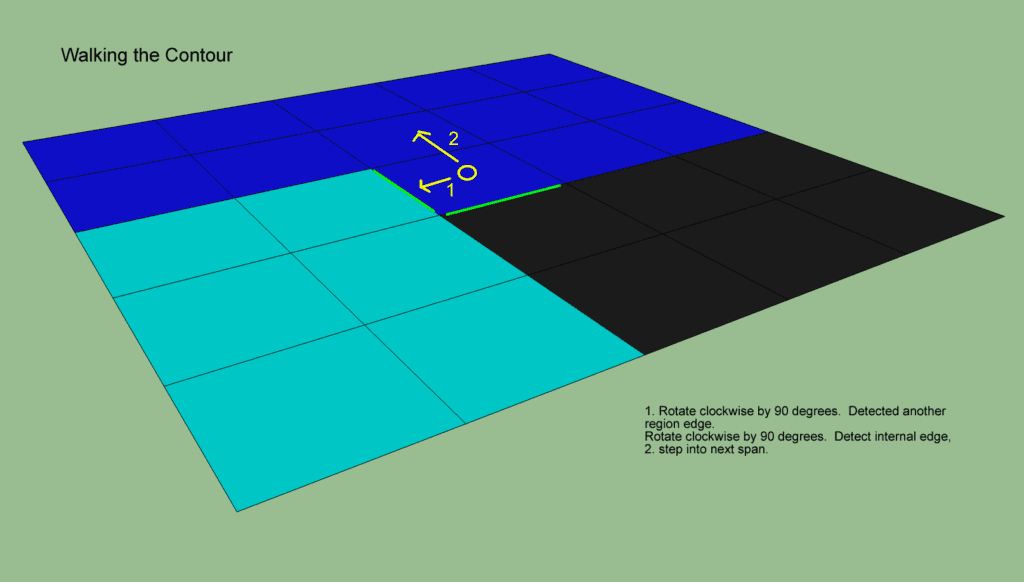
逆时针旋转90度，重复上一步操作。一直继续到我们回到起始span，面对起始方向。

从边到顶点

如果我们想回到向量空间，我们需要的是顶点，而不是边。顶点的(x, z)值很容易确定。对于每条边，我们从边沿顺时针方向取span顶部的角（corner）的(x, z)值(从span内部看)。

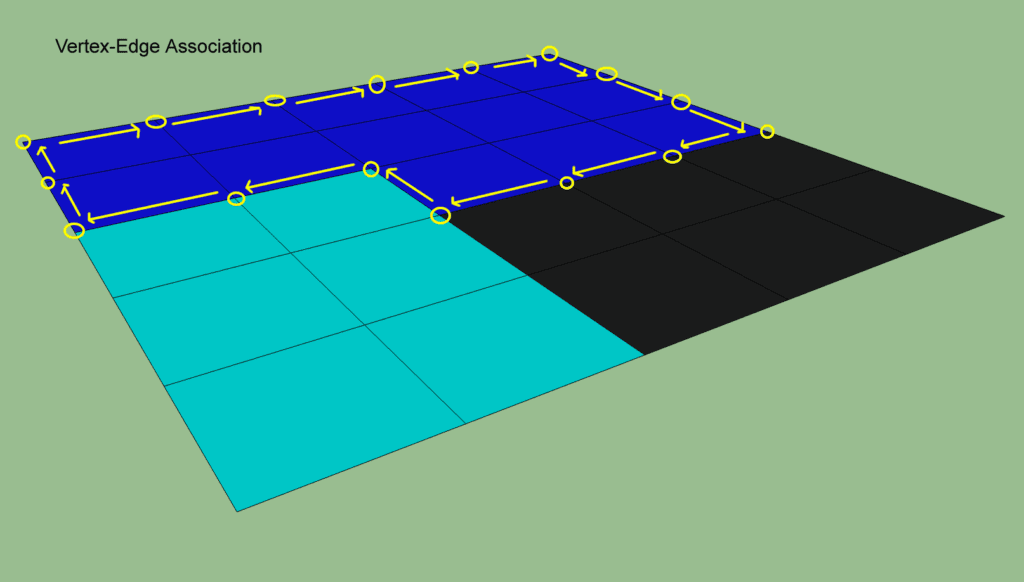
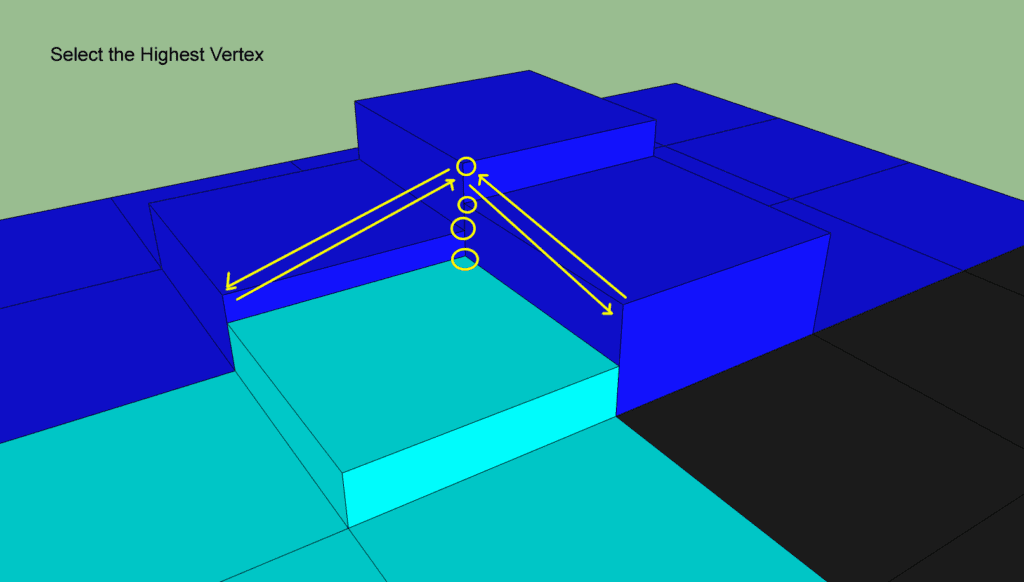
确定顶点的y值就比较棘手了。这就是我们回归3D可视化的地方。在下面的例子中，我们选择哪个顶点?

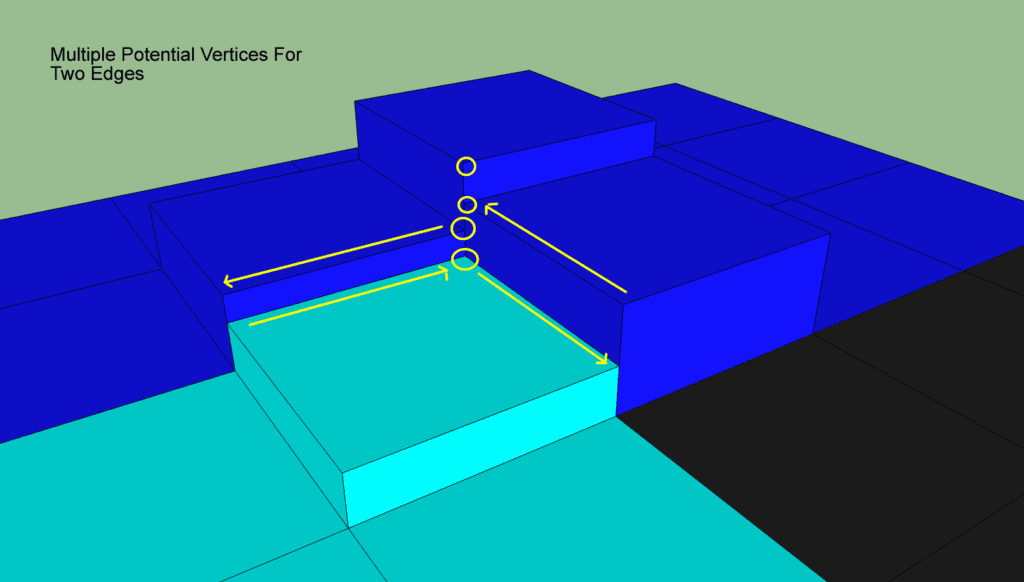
所有的边的顶点最多有四个可能的y值（译注：4个高低不同的span相邻）。选择最高的y值有两个原因：它确保最终顶点(x, y, z)位于源网格表面的上方。它还提供了一个通用的选择机制，以便所有使用该顶点的轮廓将使用相同的高度。

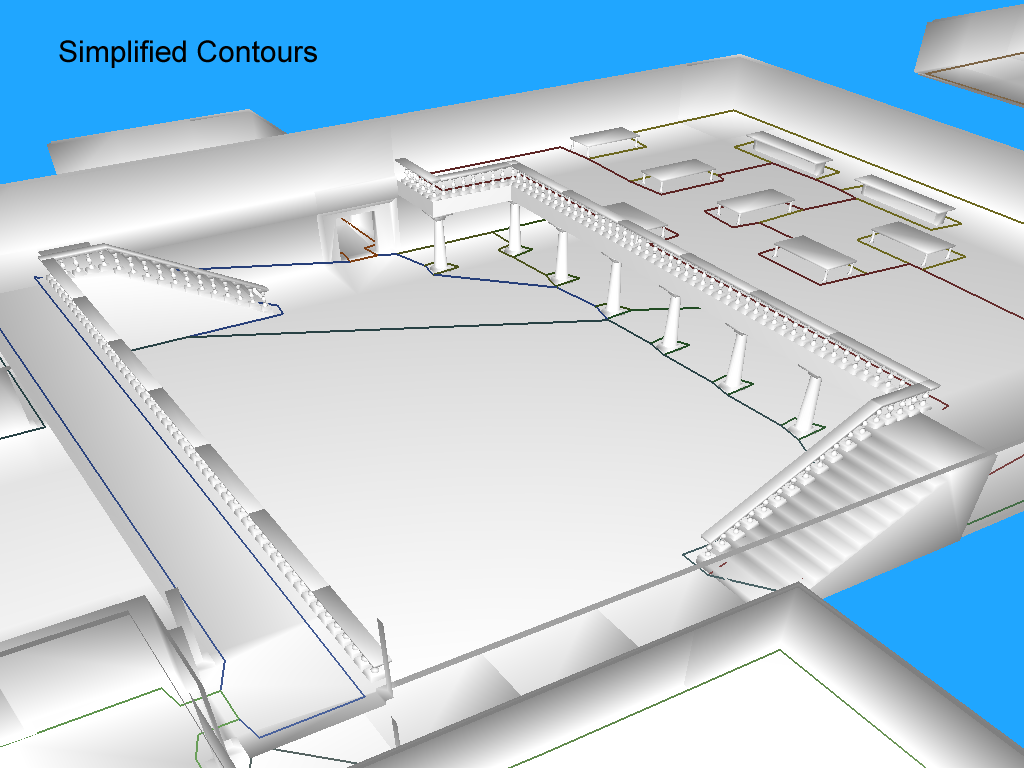
简化轮廓

至此，我们已经为所有区域生成了轮廓。轮廓是由从span的角导出的顶点所组成的。下面是一个宏观的视角。

请注意，有两种类型的轮廓部分（contour sections）。代表两个相邻区域之间门户（portal）的部分，以及与“空白”空间（"empty" space）接壤的部分。在代码的文档中，空白空间被称为“空区域”（null region），我在这里使用同样的术语。

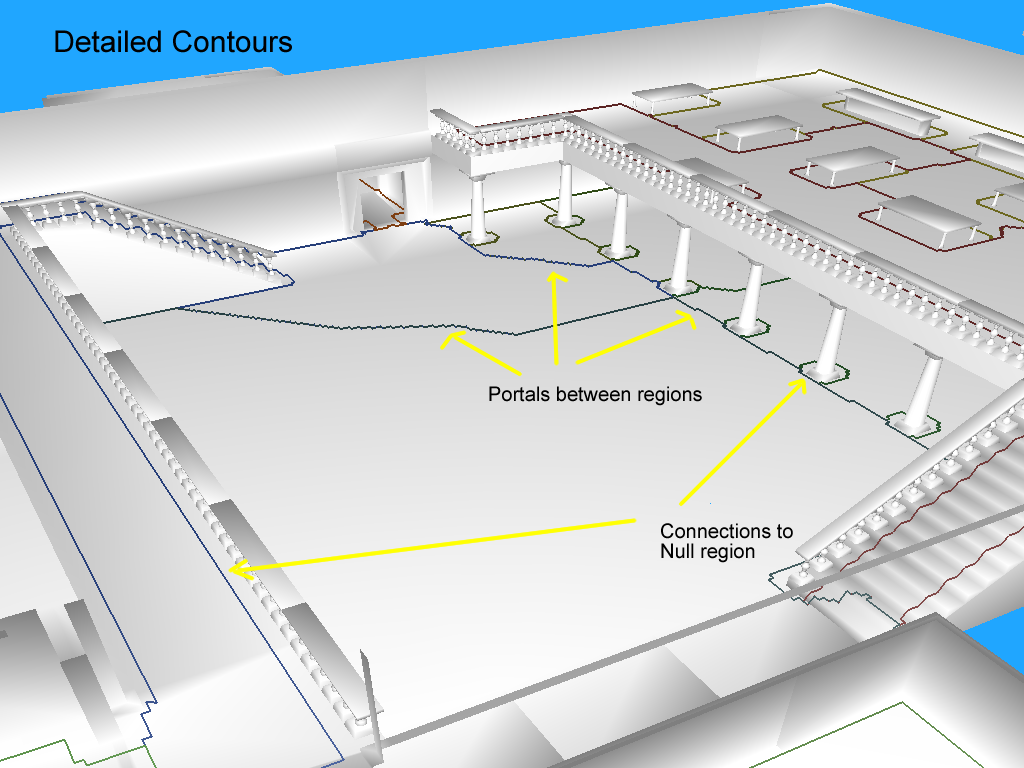
真的需要这么多顶点吗？即使在直线轮廓上，构成边的每个span都有一个顶点。显然，答案是否定的。唯一真正必需的顶点是那些在区域连接中发生变化的顶点。例如，在区域门户（portal）的边上的顶点。

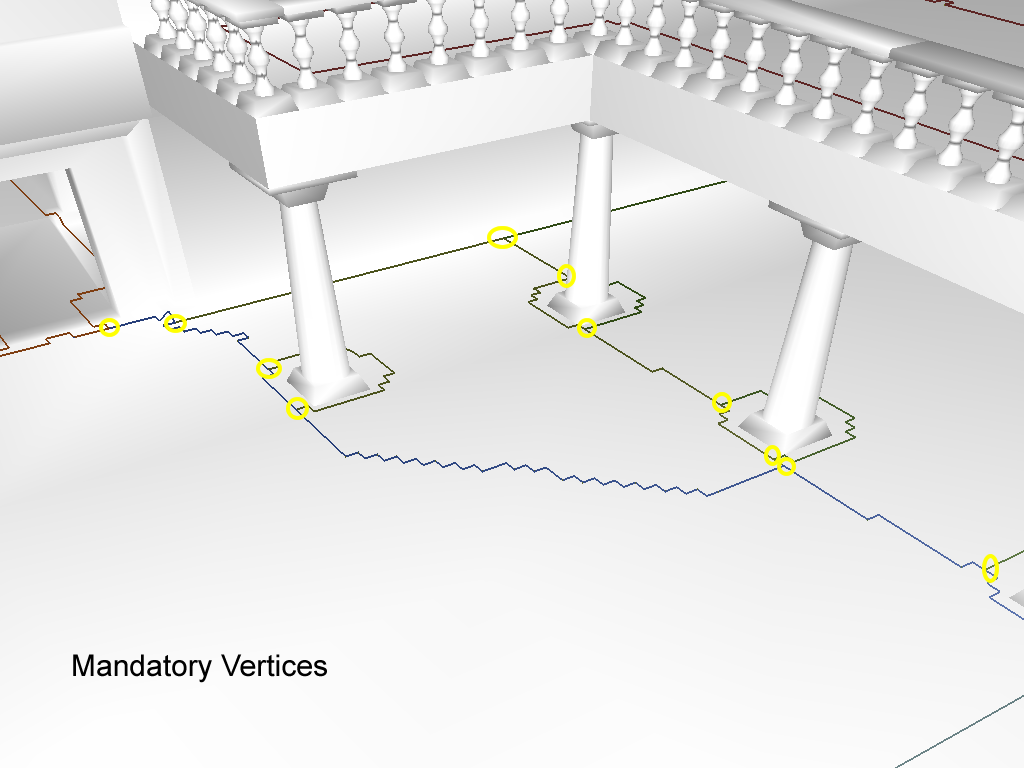
区域-区域门户（region-region portals）的简化很容易。我们丢弃除强制顶点（mandatory vertices）之外的所有顶点。

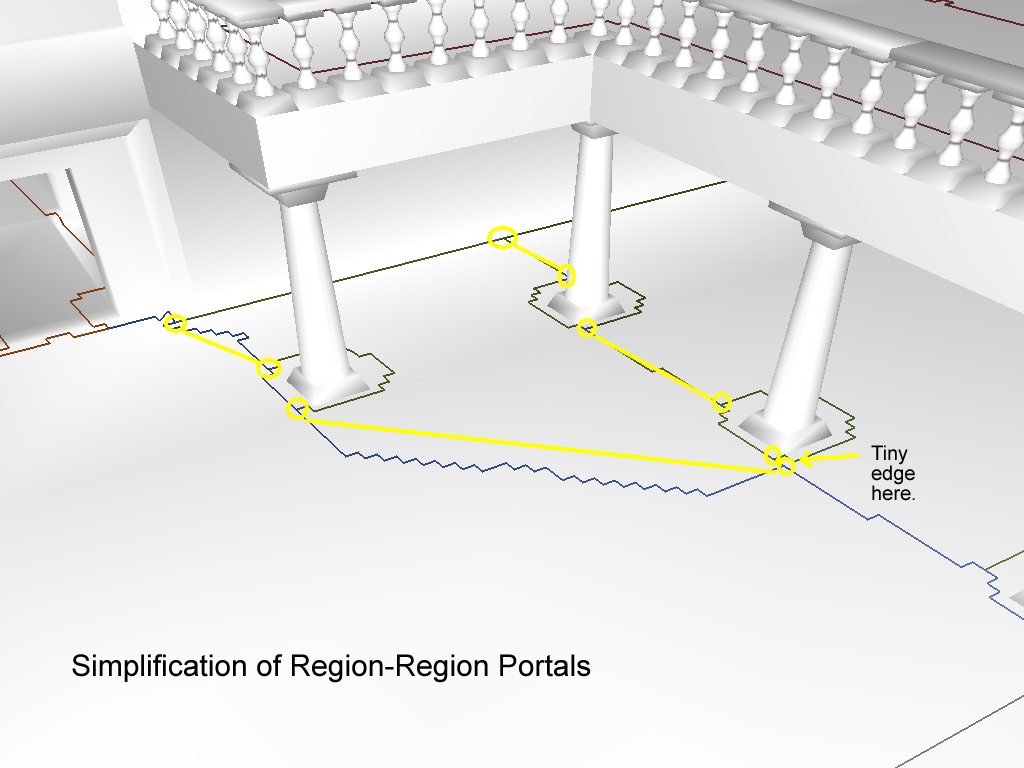
对于与空区域（null region）的连接，事情变得有点复杂了，使用了两种算法。

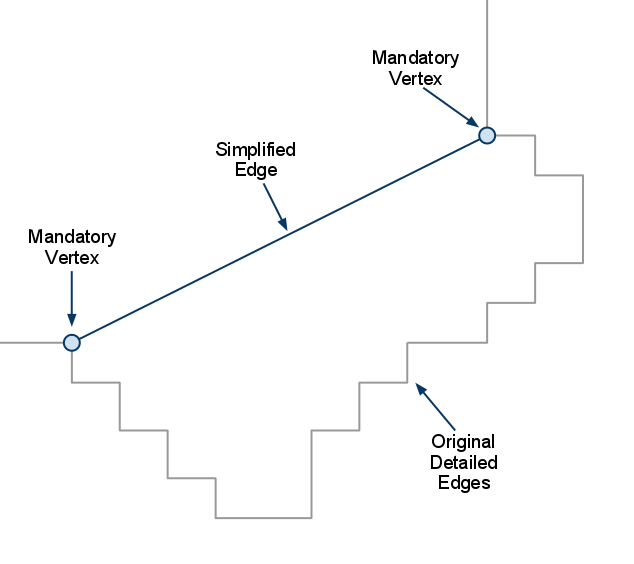
第一个是由 MatchNullRegionEdges 实现的 Douglas-Peucker 算法。 它使用 edgeMaxDeviation 参数来决定丢弃哪些顶点以得到简化的线段。它从强制顶点（mandatory vertices）开始，然后将顶点添加回来，这样原始顶点与简化边之间的距离都不会超过edgeMaxDeviation。

一步一步地来：从最简单的边开始。

找到离简化边最远的点，如果它超过了edgeMaxDeviation，则将顶点添加回轮廓。

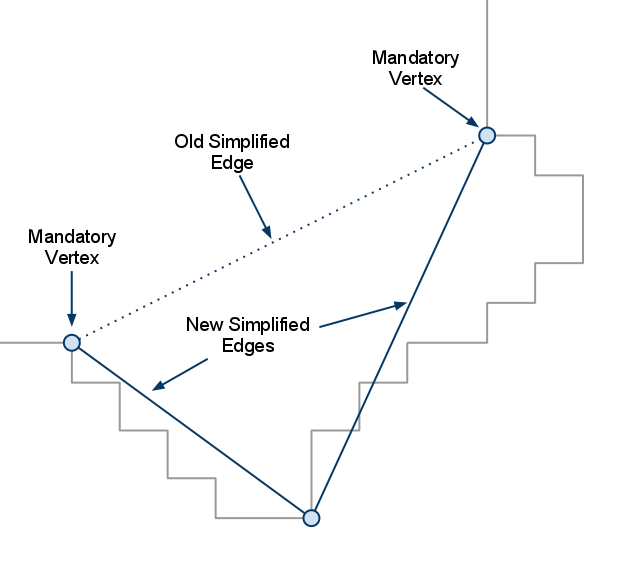
重复这个过程，直到不再有顶点到简化边的距离超过允许值。

一个简化过的轮廓示例...

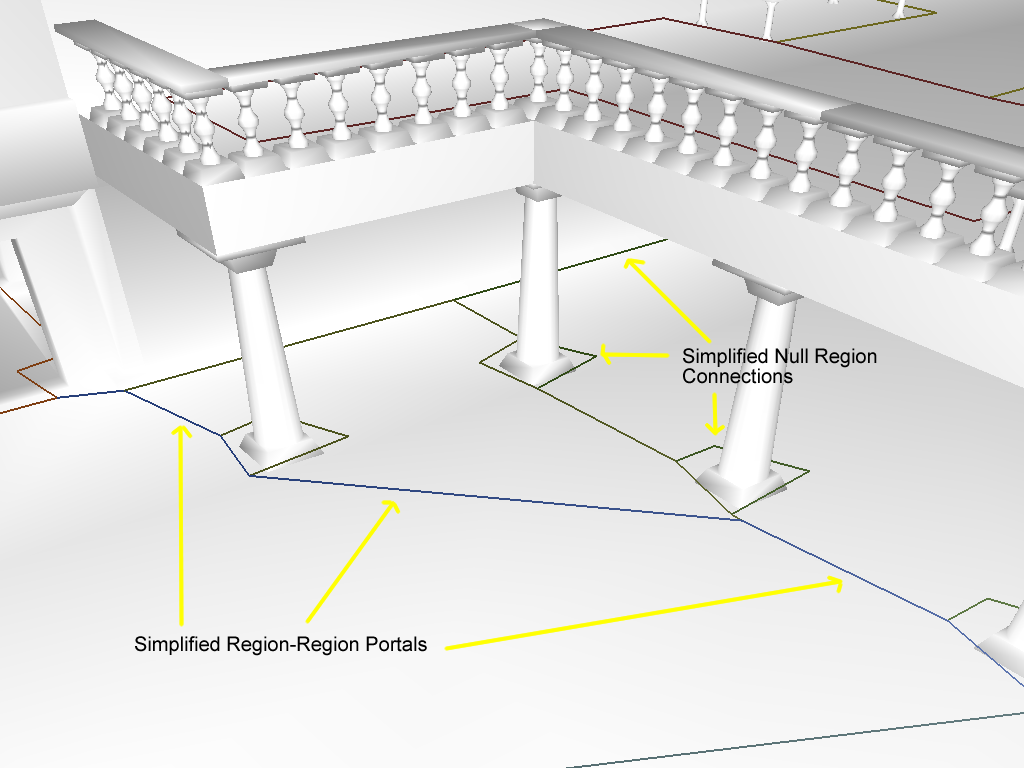
如前所述，还有一种算法用于连接到空区域（null region）的边。第一种算法可以生成长线段，以至在随后的网格生成过程中生成长而细的三角形。第二个算法由NullRegionMaxEdge实现，使用maxEdgeLength参数重新插入顶点，以确保没有线段超过最大长度。它是通过检测长边，然后将它们分成两半来实现这一点的。它会继续这个过程，直到检测不到过长的边为止。

举个例子来说明对最终网格的影响，之前…

之后...

我们在哪

在这个阶段结束时，我们有形成简化多边形的轮廓。顶点仍然在体素空间中。但是我们正在回到向量空间的路上。