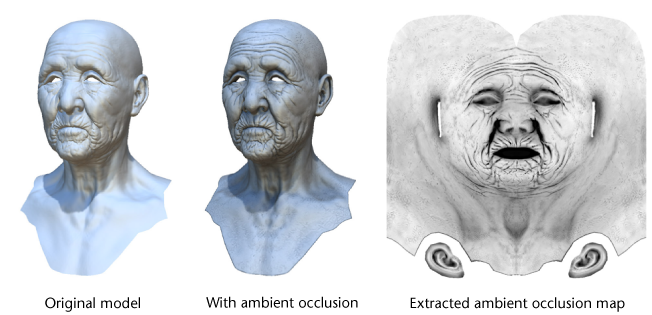
本篇文章不是特别完整,所以放上在公司做的内部分享的PPT。
SSAO月度归档: 2017 年 3 月
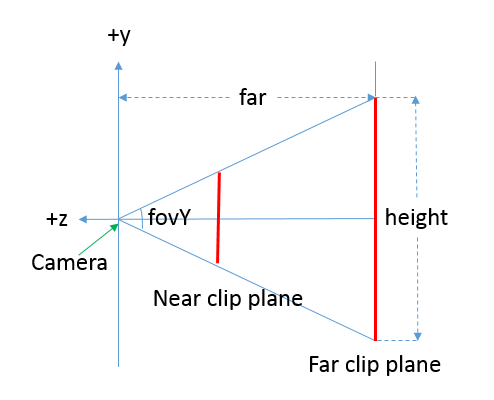

C#代码:
float fovY = m_Camera.fieldOfView;
float far = m_Camera.farClipPlane;
float height = 2 * Mathf.Tan(fovY * Mathf.Deg2Rad * 0.5f) * far;
float width = height * m_Camera.aspect;
m_Material.SetVector("_FarCorner", new Vector3(width, height, far));
上面的代码主要是求得远裁剪平面的宽、高,以及距离摄像机的距离。都是以摄像机空间的单位为单位的,而不是以像素为单位(Camera.pixelWidth, Camera.pixelHeight)。
shader代码:
float depth = Linear01Depth(tex2D(_CameraDepthTexture, uv).x); float3 ray = (half3(-0.5f,-0.5f,0) + half3(uv.xy,-1)) * _FarCorner; float3 viewPos = ray * depth;
tex2D(_CameraDepthTexture, uv).x根据屏幕像素的uv对深度纹理进行采样获取Z buffer,但此时的Z buffer是非线性的,需要调用Linear01Depth将其映射到线性的[0, 1]区间内,0对应摄像机位置,1对应远裁剪平面。
half3(-0.5f,-0.5f,0) + half3(uv.xy,-1)将uv坐标减去0.5,从[0,1]区间映射到了[-0.5,0.5]区间。
乘以_FarCorner得到half3((uv.x - 0.5f) * width, (uv.y - 0.5f) * width, -1 * far),此时x在[-0.5width, 0.5width]区间内,y在[-0.5height, 0.5height]区间内,z是-far。
但以上只是远裁剪平面的情况,实际上每个xy平面的宽高以及对应的z值是随depth线性变化的。所以最后一步乘以depth,获得最终的摄像机空间下的坐标。

概念
Lambertian反射定义了一个理想的无光表面或者漫反射表面。无论观察者的视角如何,Lambertian表面对观察者表现的亮度都是相同的。
也就是说, 表面的亮度是各向同性的,并且发光强度遵循Lambert的余弦定律。
在计算机图形学中,Lambertian反射一般被用于漫反射模型。
公式

I_d=L \cdot N C I_L
其中:
I_d:表面的漫反射强度L:表面指向光源的向量(归一化)N:表面的法线向量方向(归一化)C:表面颜色I_L:入射光的强度(也即光的RGB)
根据公式可以看出反射的强度跟视角无关,跟法线和光源方向的夹角的余弦值(即L \cdot N)成正比。
当N和L之间的夹角超过90度也就是在背光的一面,L \cdot N的结果会小于零,这种情况下一般直接取0(即max(0,L \cdot N)),所以看起来会比较平。Valve公司在开发Half Life时,对Lambert模型做了简单的修改,以避免这种问题的发生:
变种:Half Lambert
Half-Life中首先使用的技术,对Lambert模型进行了简单的修改,避免物体的背光面看起来太平。方式是将max(0,L \cdot N)改为0.5(L \cdot N)+0.5,即将点积的结果由[-1,1]变为[0,1]。
To soften the diffuse contribution from local lights, the dot product from the Lambertian model is scaled by ½, add ½ and squared.
Value官方对Half Lambert的解释中好像还说了要平方,但网上的各种实现都没有这一步,不知道是不是理解错了squared的意思。如果不平方,Half Lambert要比Lambert亮很多,平方之后就比较接近了:

法线方向和光源方向的夹角从0到π变化时,三种情况的曲线,黑色Lambert,红色Half Lambert,绿色Half Lambert Squared: